2025.3.22NCTF

是 2025.3.22NCTF 哒！

爆0了…所以给出的我自己的脚本有些是不会与靶机交互的，但最后会给出官方的wp
才不是我懒得写

绮云

花灯百盏遥遥一线牵

from Crypto.Util.number import *
from os import getenv,urandom
from hashlib import sha256
from random import randint

class ECDSA:
    def __init__(self):
        self.p = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF
        self.a = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC
        self.b = 0x28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93
        self.n = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
        self.Gx = 0x32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7
        self.Gy = 0xBC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0
        self.G = (self.Gx,self.Gy)

        self.d = getPrime(232)
        self.Q = self.mul(self.d,self.G)
        assert self.is_on_curve(self.Q)

    def is_on_curve(self, point):
        if point is None:
            return True
        x, y = point
        return (y**2 - x**3 - self.a * x - self.b) % self.p == 0

    def add(self, p1, p2):
        if p1 is None or p2 is None:
            return p1 if p2 is None else p2

        x1, y1 = p1
        x2, y2 = p2

        if x1 == x2 and y1 != y2:
            return None
        if x1 == x2:
            m = (3 * x1 * x1 + self.a) * pow(2 * y1, -1,  self.p) % self.p
        else:
            m = (y2 - y1) * pow((x2 - x1) % self.p, -1, self.p) % self.p
        
        x3 = (m * m - x1 - x2) % self.p
        y3 = (m * (x1 - x3) - y1) % self.p
        return (x3, y3)

    def mul(self, k:int, P:tuple[int,int]):
        if P is None:
            return None
        
        R = None        
        while k > 0:
            if k & 1:
                R = self.add(R, P)
            P = self.add(P,P)
            k >>= 1
        return R

    def generate_key_pair(self):
        return self.d,self.Q

    def sign(self, message):
        while True:
            k = randint(1, self.n - 1)
            P = self.mul(k, self.G)
            if P is None:
                continue
            
            r = P[0] % self.n
            if r == 0:
                continue

            s = (pow(k,-1,self.n) * (int.from_bytes(sha256(message).digest())+ self.d * r)) % self.n
            if s != 0:
                return (r, s)

    def verify(self, m:bytes, r:int,s:int):
        if not (1 <= r < self.n and 1 <= s < self.n):
            return False
        
        u1 = (int.from_bytes(sha256(m).digest()) * pow(s,-1,self.n)) % self.n
        u2 = (r * pow(s,-1,self.n)) % self.n

        if u1 == 0 or u2 == 0:
            return False

        P = self.add(self.mul(u1, self.G), self.mul(u2, self.Q))        
        return P[0] % self.n == r

class RSA:
    def __init__(self,d:int):
        p = getStrongPrime(1024)
        q = getStrongPrime(1024)
        
        assert GCD(d,(p-1)*(q-1)) == 1

        self.N = p * q
        self.d = d
        self.e = pow(d,-1,(p-1)*(q-1))

    def encrypt(self,m:int,idx:int):
        return pow(m,self.e ^ (1 << idx),self.N)
    
def check():
    r,s = list(map(int,input('Give me your signature:').split()))
    if e.verify(f'nctf2024-{urandom(1).hex()}'.encode(),r,s):
        print(f'Congratulations! Here is your flag: {getenv("FLAG")}')
        exit()
    else:
        print('Wrong!')


if __name__=='__main__':
    e = ECDSA()
    print('Can you navigate yourself through QiYun Valley with only the encryption orcale?')

    menu = '''
--- Menu ---
[1] Initialize encryption orcale
[2] Check your signature
[3] Exit'''

    while True:
        print(menu)
        opt = input('Your option:').strip()
        
        if opt=='1':
            print('Generating new public key pair for you...')
            rsa = RSA(e.d ** 4)

            while input("Enter 'e' for encryption or other to exit:").strip() == "e":
                m = int(input('Enter your message:'),16)
                x = int(input('Where do you want to interfere?'))

                print(f'Result:{hex(rsa.encrypt(m,x))[2:]}')

        elif opt=='2':
            check()
        
        elif opt=='3':
            print('Bye~')
            exit()

        else:
            print('Invalid option')

题目允许我们:1.翻转e的任意一个比特位然后进行加密，返回加密结果;2.检查椭圆曲线的签名，正确就给flag。而椭圆曲线的d的4次方就是RSA的d。
我们需要通过明文和密文来推出e和n，进而推出d，再进行轻度的签名爆破即可。
首先要获取RSA的n。我是在lazzaro的博客里找到了这个
选择明/密文攻击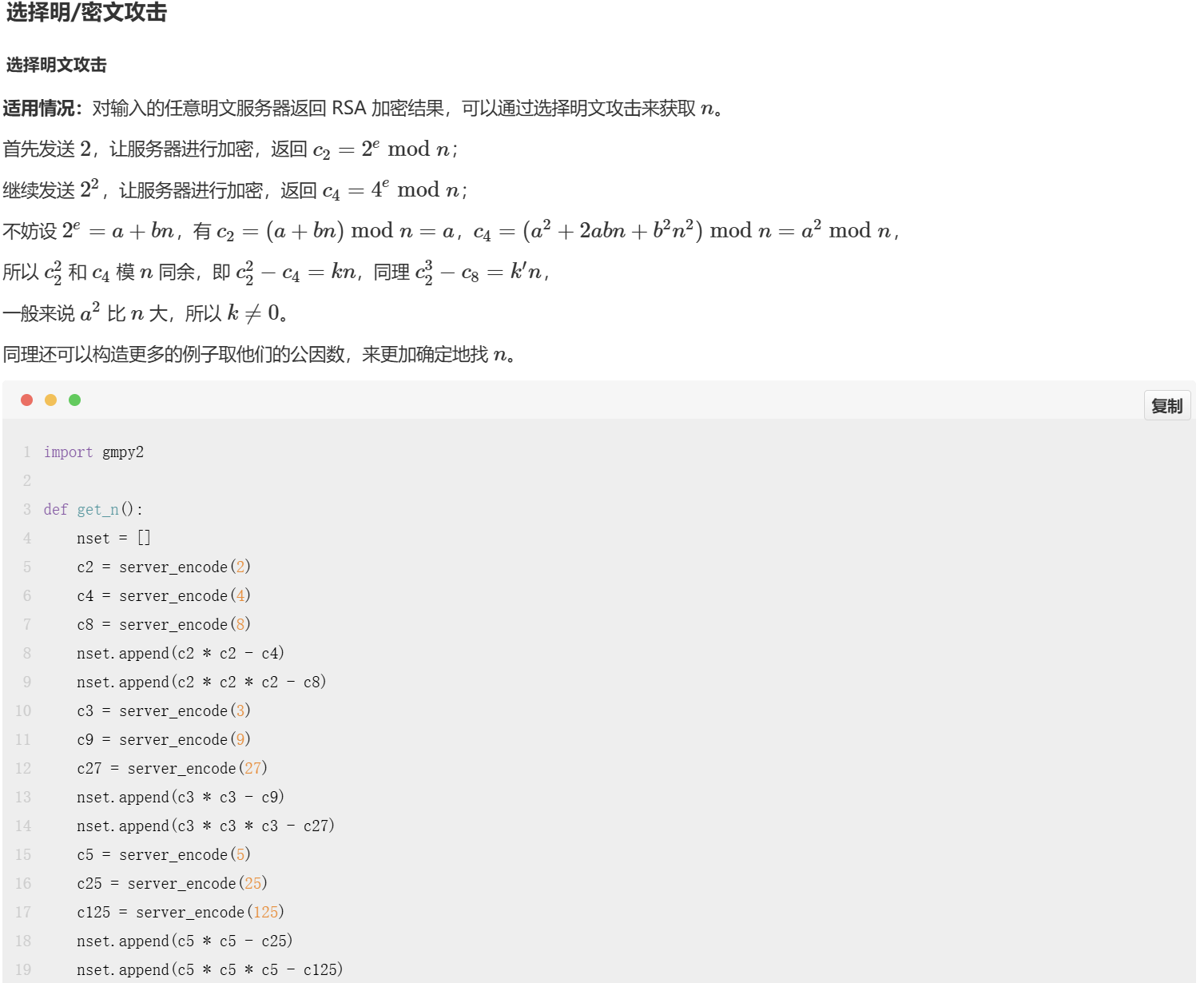

让服务器加密明文P，得到结果C1，再加密明文P**2，得到结果C2，那么就能得到C1**2-C2=kn，再对另一个明文P2重复操作即可得到k'n，对这两个结果求GCD即可得到n，可能会有一些小素数因子存在，去掉即可。
由题可知GCD(e,(p-1)*(q-1))=1，所以e一定是奇数，那么e的最低比特位一定是1。
我们就可以翻转最低比特位，再对2进行加密，返回的结果一定是2**(e-1)%n，结果再乘2模n即是2**e%n，我们就得到了未翻转任何比特位的加密结果。
之后，我们再继续翻转第k位比特位，把加密结果乘2**(1<<k)再模n，这个操作相当于把e的第k位加1。
如果这个比特位翻转前是1，那么翻转后就是0，加1后又变回了1，也就是说会得到未翻转比特位的e的加密结果。
所以，当我们把加密结果乘以2**(1<<k)后再模n，如果密文与前面得到的未翻转任何比特位的加密结果相同，说明这个比特位是1，反之是0
这里给出我比赛时用的得到n和e的脚本。

from Crypto.Util.number import *
from pwn import *
from sympy import nextprime

def t(m:int,x:int):
    m=hex(m)[2:].encode()
    x=str(x).encode()
    out=r.recvuntil(b':')
    r.sendline(b'e')
    out=r.recvuntil(b':')
    r.sendline(m)
    out=r.recvuntil(b'?')
    r.sendline(x)
    out=r.recvuntil(b'\n')
    out=int(out.decode()[:-2].split(':')[-1],16)
    return out
    
context.log_level = 'debug'
r=remote('39.106.16.204',16330)

out=r.recv(400)
print(out)

r.sendline(b'1')
out=r.recvuntil(b'\n')
print(out)

c2=t(2,0)
c4=t(4,0)

c3=t(3,0)
c9=t(9,0)

c5=t(5,0)
c25=t(25,0)

n1=c2**2-c4
n2=c3**2-c9
n3=c5**2-c25

n_=GCD(n1,n2)
n=GCD(n_,n3)

#检查是否有小素数因子，其实可能不需要检查这么多
pri=2
for i in range(100):
    while n%pri==0:
        n//=pri
    pri=nextprime(pri)

print(n)

#得到未翻转比特位的加密结果
c=c2*2%n

e=[0]*2049

for i in range(2049):
    if i%200==0:
        print(i)
    if t(2,i)*pow(2,1<<i,n)%n==c:
        e[i]=1
    else:
        e[i]=0

e=int(''.join(map(str,e[::-1])),2)
print(e)

得到n,e后就不会了…
看了下wp是用格的，而且需要10组n,e，也就是说交互时间是非常长的。
wp的解释:

这是我复现的脚本:

import gmpy2
#10组n和e
el=[]
nl=[]

length=11
B=[[0]*length for i in range(length)]
for i in range(len(B)-1):
    B[i][i]=nl[i]
    B[-1][i]=el[i]
B[-1][-1]=2^1024
B=matrix(ZZ,B)
B_=B.LLL()

d=B_[0][-1]//2^1024
d=gmpy2.iroot(d,4)
print(d)
d=d[0]

(mpz(3650017291377232489980231598072561018897386229012755703758171135449773), True)

成功得到d。
之后用题目中的sign函数对随机一个byte签名即可，然后尝试verify，直到靶机随机到你签名的那个byte。
官方wp:

#sage
__import__('os').environ['TERM'] = 'xterm'

from pwn import *
from sage.all import *
from time import time
from hashlib import sha256

io = remote('39.106.16.204', 10645)
# io = process(['python3', 'task.py'])

nls = []
els = []

recv_hexint = lambda: int(io.recvline().strip().decode(), 16)

t0 = time()

for _ in range(10):
    io.sendlineafter(b'option:', b'1')
    # decipher N via GCD

    numls = []
    for i in range(9):
        msg = int(1 << (i + 1)).to_bytes(2, 'big')
        io.sendlineafter(b'exit:', b'e')
        io.sendlineafter(b'message:', msg.hex().encode())
        io.sendlineafter(b'interfere?', b'0')
        io.recvuntil(b'Result:')
        numls.append(int(io.recvline().strip().decode(), 16))

    gcdls = []
    for i in range(1, 9):
        gcdls.append(numls[0] ^ (i + 1) - numls[i])

    n = gcd(gcdls)
    nls.append(n)
    print(f'n #{_} = {n}')

    # decipher e via fault injection of e

    orcale_msg = 3

    io.sendlineafter(b'exit:', b'e')
    io.sendlineafter(b'message:', int(orcale_msg).to_bytes(1, 'big').hex().encode())
    io.sendlineafter(b'interfere?', b'2048')
    io.recvuntil(b'Result:')
    basis = recv_hexint() * pow(orcale_msg, -2**2048, n) % n  # basis, = pow(m,e,n)

    e_rng = [0] * 2048

    for i in range(2048):
        io.sendlineafter(b'exit:', b'e')
        io.sendlineafter(b'message:', int(orcale_msg).to_bytes(1, 'big').hex().encode())
        io.sendlineafter(b'interfere?', str(i).encode())
        io.recvuntil(b'Result:')

        temp = recv_hexint()
        multiplier = pow(orcale_msg, 2**i, n)

        if temp == basis * multiplier % n:  # 0 -> 1, original = 0
            e_rng[i] = 0
        else:  # 1 -> 0, original = 1
            assert temp == basis * pow(multiplier, -1, n) % n  # ensure
            e_rng[i] = 1

    e_res = int(''.join(str(i) for i in e_rng)[::-1], 2)
    assert pow(orcale_msg, e_res, n) == basis
    els.append(e_res)

    print(f'e #{_} = {e_res}')
    print(f'Time elasped: {time() - t0:.2f}s')
    io.sendlineafter(b'exit:', b'')

const = 2**1024
mt = matrix.diagonal(ZZ, nls + [0]).dense_matrix()
mt[-1] = els + [const]
mt = mt.LLL()

temp = abs(mt[0, -1])
assert temp % const == 0
d = ZZ(temp / const)

x = d.nth_root(4)
E = EllipticCurve(Zmod(0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF), [0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC, 0x28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93])
n = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123

G = E((0x32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7, 0xBC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0))
m0 = int.from_bytes(sha256('nctf2024-00'.encode()).digest(), 'big')

while True:
    k = int(time() * 1000)  # any random number smaller than n
    P = k * G
    r = int(P.xy()[0]) % n
    s = (pow(k, -1, n) * (m0 + x * r)) % n
    if r != 0 and s != 0:
        break

send = f'{r} {s}'.encode()
while True:
    io.sendlineafter(b'option:', b'2')
    io.sendlineafter(b':', send)
    msg = io.recvline()
    if b'flag' in msg:
        print(msg.decode())
        break

io.close()

Sign

这是恢复互联网的密钥，密码是实时生成的三万个随机数。
srv.py:

from Crypto.Util.number import *
from util import *
from os import getenv
from Crypto.Util.Padding import pad
from random import Random
from Crypto.Cipher import AES
from hashlib import md5

string = open('secret.txt').read().strip().encode()
flag = getenv('FLAG').encode()

if __name__=='__main__':
    Keys = []
    for m in string:
        f = FHE()
        s = long_to_bytes(Random().getrandbits(20000))
        for i in s[4:]:
            Keys.extend(f.encrypt([i]))

        for i in s[:4]:
            Keys.extend(f.encrypt([i * (m & 0x03) % 0x101]))
            m >>= 2
        
    assert len(Keys) == 30000

    print(f'[+] Your ciphertext: {AES.new(md5(string).digest(),AES.MODE_ECB).encrypt(pad(flag,16)).hex()}')
    input(f'[+] The keys to retrieve the global internet connection are as follows:')
    for i in range(30000):
        print(f'[+] {Keys[i]}')

util.py:

from os import urandom
from Crypto.Util.number import *

def getrandint(n:int):
    return int.from_bytes(urandom(n//8+1)) % pow(2,n)

class FHE:
    def __init__(self):
        self.p = getPrime(77)
        self.pubkeys = []
        for _ in range(16):
            self.pubkeys.append(self.p * getrandint(177) + (getrandint(17) << 8))

    def encrypt(self,msg:list[int] | bytes):
        result = []
        for m in msg:
            tmp = 0
            shuffle_base = urandom(16)
            for i in shuffle_base:
                x,y = divmod(i,16)
                tmp += x*self.pubkeys[y] + y*self.pubkeys[x]
            result.append(tmp + m)
        return result

题目的意思很简单，恢复字符串string，然后解密AES即可。
通过观察FHE的encrypt函数，我们不难得出msg=result%p%256
result%p能得到getrandint(17) << 8+m，而getrandint(17) << 8的低8位正好是0，%256即可得到msg。
求出mag后我们就可以恢复s[4:]的值了，并且因为这20000bits是通过random模块生成的，random模块采用的是MT19937作为伪随机数生成器的，所以我们可以逆向MT19937来获得s[:4]
得到了s[:4]后我们就可以恢复string了，具体细节之后再说
所以问题就变成了如何得到p。
嗯…比赛时卡这了，所以来看wp吧~



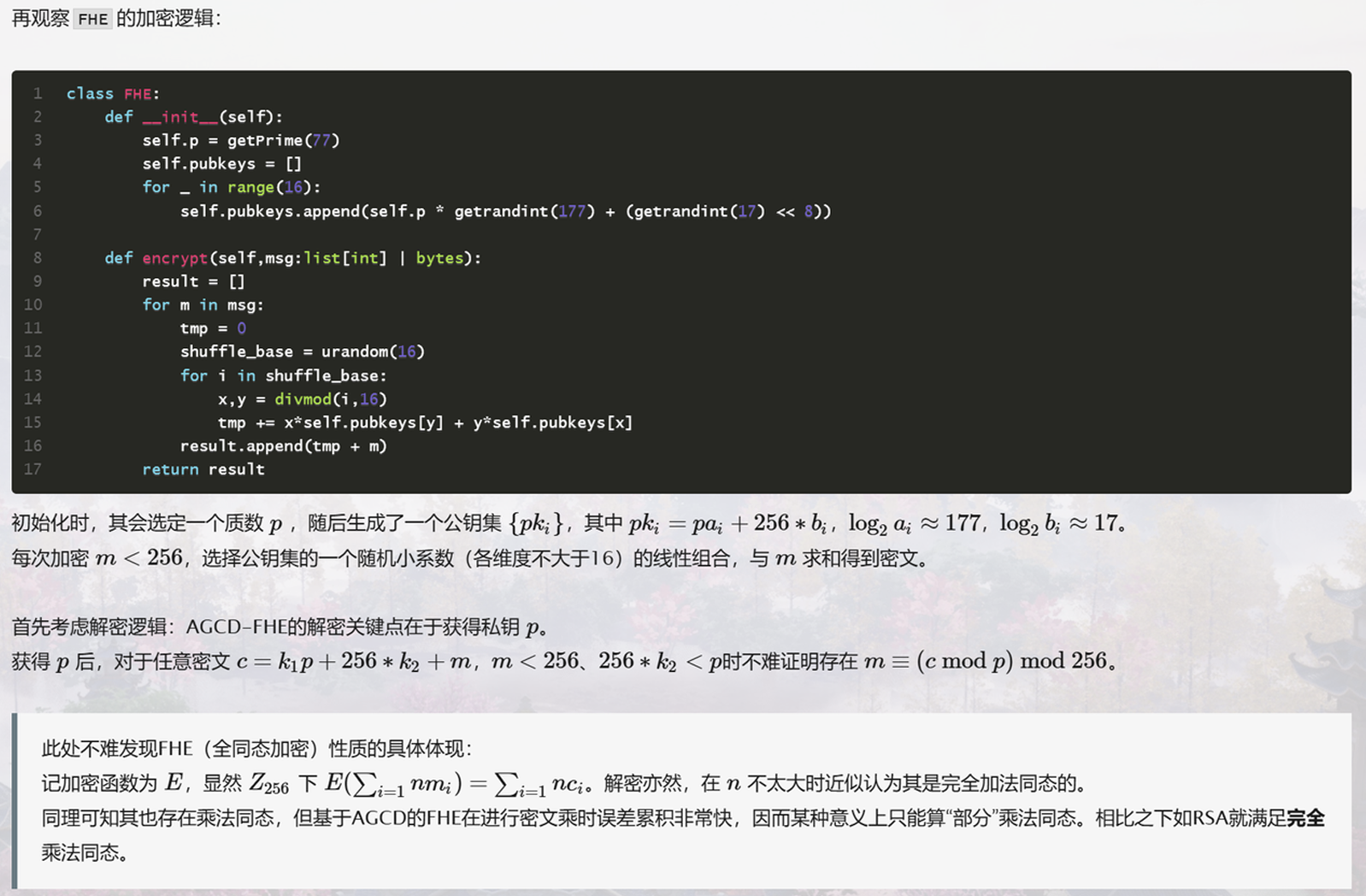
这是一个求近似最大公约数问题(AGCD/Approximate Greatest Common Divisor)。
所以，上格。

x0=p*q0+e0+m0
xi=p*qi+ei+mi
->
x0*qi=p*q0*qi+(e0+m0)*qi
xi*q0=p*qi*q0+(ei+mi)*q0
两式相减
x0*qi-xi*q0=(e0+m0)*qi-(ei+mi)*q0

我们通过构造上面的格就可以还原出q0，进而求出p。
值得一提的是求出来的q0需要abs一下，因为LLL求出来的是最短向量，是有可能为负的，相比之下BKZ求出负值的概率就小一点了，但依旧存在。以及格中的短向量2**(ρ+1)的值在很大程度上并不影响结果，取1都可以。
这里给出我复现时的求p的脚本:

Keys=[]
B=[[0]*length for i in range(length)]
for i in range(length-1):
    B[i][i]=Keys[j*2500+0]
    B[-1][i]=Keys[j*2500+i+1]
B[-1][-1]=k
B=matrix(ZZ,B)
B_=B.LLL()

q0=abs(B_[0][-1])//k
p=((Keys[j*2500]-Keys[j*2500]%q0)//q0)

求出p后我们就可以得到s[4:]
接下来需要求出s[:4]
这里涉及到random生成固定位数的随机数的方式
下面的拼接都是以16进制字符串的形式进行的拼接，不是加法
对于32位以下的随机数，比如getrandbits(16)，random会先生成32位的随机数然后截断，只取前16位然后return
对于32位以上的随机数，比如getrandbits(64)，random会生成2个32位是随机数，再进行拼接，后生成的随机数拼接在先生成的随机数的前面，即后生成的32位随机数+先生成的32位随机数，对于不是32的倍数的bits的随机数，比如getrandbits(80)，random会先按前面的方法生成64位随机数，再按32位一下的随机数的生成方法来生成16位的随机数，后生成的永远排在先生成的前面，即截断成16位的第3次生成的随机数+32位的第2次生成的随机数+32位的第1次生成的随机数
所以，得到s[:4]的方法很明确了，通过s[4:]来逆向MT19937，然后再生成一个32位的随机数就是s[:4]了。
我复现的时候就是没弄清楚然后调了好久，一直以为s[:4]是最先生成的32位随机数，还找了相关的脚本，这里顺便也贴一下:

import random

def inv_shift_right(x:int,bit:int,mask:int = 0xffffffff) -> int:
    tmp = x 
    for _ in range(32//bit):
        tmp = x ^ tmp >> bit & mask
    return tmp

def inv_shift_left(x:int,bit:int,mask:int = 0xffffffff) -> int:
    tmp = x
    for _ in range(32//bit):
        tmp = x ^ tmp << bit & mask
    return tmp

def rev_extract(y:int) -> int:
    y = inv_shift_right(y,18)
    y = inv_shift_left(y,15,4022730752)
    y = inv_shift_left(y,7,2636928640)
    y = inv_shift_right(y,11)
    return y

def backtrace_untwist(cur):
    high = 0x80000000
    low = 0x7fffffff
    mask = 0x9908b0df
    state = cur
    for i in range(623,-1,-1):
        tmp = state[i]^state[(i+397)%624]
        # recover Y,tmp = Y
        if tmp & high == high:
            tmp ^= mask
            tmp <<= 1
            tmp |= 1
        else:
            tmp <<=1
        # recover highest bit
        res = tmp&high
        # recover other 31 bits,when i =0,it just use the method again it so beautiful!!!!
        tmp = state[i-1]^state[(i+396)%624]
        # recover Y,tmp = Y
        if tmp & high == high:
            tmp ^= mask
            tmp <<= 1
            tmp |= 1
        else:
            tmp <<=1
        res |= (tmp)&low
        state[i] = res    
    return state
def exp_mt19937(output:list) -> int:
    assert len(output) == 624
    cur_stat = [rev_extract(i) for i in output]
    return cur_stat

random.seed(1)
l=[random.getrandbits(32) for i in range(624)]
stat=exp_mt19937(l)
stat=backtrace_untwist(stat)
r=random.Random()
r.setstate((3, tuple(stat + [624]), None))
assert r.getrandbits(32)==l[0]
#要求l序列之前的值，只需要更改setstate里面的624即可，每减一就是向前推一个
r.setstate((3, tuple(stat + [623]), None))
r.getrandbits(32)
assert r.getrandbits(32)==l[0]

这里提一下，random每生成624个随机数后就会调用一次twist来更新内部的state，也就是说我们向前面逆向每624个随机数就要调用一次backtrace_untwist。不明白的可以自己尝试一下，这里不多说了。
好的，我们回到题目中去。
刚刚我们做到了逆向MT19937这一步，接下来我们需要的就是用s[4:]来逆向获取MT19937的内部状态，然后再根据这个来得到下一个32位的随机数，就是s[:4]，逆向MT19937的方法我目前知道2个，一个是用randcrack这个库，你只需要提交624个32位的随机数，然后调用predic_getrandbits(32)即可，挺方便的。另一个就是用和上面差不多的脚本，只不过就是不需要调用backtrace_untwist来转换状态了。把exp_mt19937返回的state直接传入r.setstate里即可。
这里给出我复现时的脚本。

from Crypto.Util.number import *
from hashlib import md5
from Crypto.Cipher import AES
from random import Random

def inv_shift_right(x:int,bit:int,mask:int = 0xffffffff) -> int:
    tmp = x 
    for _ in range(32//bit):
        tmp = x ^^ tmp >> bit & mask
    return tmp

def inv_shift_left(x:int,bit:int,mask:int = 0xffffffff) -> int:
    tmp = x
    for _ in range(32//bit):
        tmp = x ^^ tmp << bit & mask
    return tmp

def rev_extract(y:int) -> int:
    y = inv_shift_right(y,18)
    y = inv_shift_left(y,15,4022730752)
    y = inv_shift_left(y,7,2636928640)
    y = inv_shift_right(y,11)
    return y

def backtrace_untwist(cur):
    high = 0x80000000
    low = 0x7fffffff
    mask = 0x9908b0df
    state = cur
    for i in range(623,-1,-1):
        tmp = state[i]^^state[(i+397)%624]
        # recover Y,tmp = Y
        if tmp & high == high:
            tmp ^^= mask
            tmp <<= 1
            tmp |= 1
        else:
            tmp <<=1
        # recover highest bit
        res = tmp&high
        # recover other 31 bits,when i =0,it just use the method again it so beautiful!!!!
        tmp = state[i-1]^^state[(i+396)%624]
        # recover Y,tmp = Y
        if tmp & high == high:
            tmp ^^= mask
            tmp <<= 1
            tmp |= 1
        else:
            tmp <<=1
        res |= (tmp)&low
        state[i] = res    
    return state

def exp_mt19937(output:list) -> int:
    assert len(output) == 624
    cur_stat = [rev_extract(i) for i in output]
    r = Random()
    r.setstate((3, tuple([int(i) for i in cur_stat] + [624]), None))
    return r

length=21
k=1
string=b''
for j in range(12):
    B=[[0]*length for i in range(length)]
    for i in range(length-1):
        B[i][i]=Keys[j*2500+0]
        B[-1][i]=Keys[j*2500+i+1]
    B[-1][-1]=k
    B=matrix(ZZ,B)
    B_=B.LLL()

    q0=abs(B_[0][-1])//k
    p=((Keys[j*2500]-Keys[j*2500]%q0)//q0)
    #p=p+p%2-1
    print(p)

    ilist=[Keys[j*2500+i]%p%256 for i in range(2500)]
    r=exp_mt19937([bytes_to_long(bytes(ilist[i:i+4])) for i in range(0,2496,4)][::-1])
    s=list(long_to_bytes(r.getrandbits(32)))
    __l=[]
    for i in range(4):
        if s[i]!=0:
            m_=ilist[2496+i]*inverse(s[i],0x101)%0x101
            __l+=[bin(m_)[2:].zfill(2)]
        else:
            __l+=['00']
    __l=__l[::-1]
    m=long_to_bytes(int(''.join(__l),2))
    print(m)
    string+=m
print(string)
print(AES.new(md5(string).digest(),AES.MODE_ECB).decrypt(long_to_bytes(int(cipher,16))))

官方wp(官方wp里没有对求出来的q取abs):

# sage
__import__('os').environ['TERM'] = 'xterm'
from sage.all import *
from Crypto.Util.number import *
from functools import reduce
from random import *
from pwn import *
from Crypto.Util.Padding import unpad
from Crypto.Cipher import AES
from hashlib import md5


def inv_shift_right(x: int, bit: int, mask: int = 0xffffffff) -> int:
    tmp = x
    for _ in range(32 // bit):
        tmp = x ^ tmp >> bit & mask
    return tmp


def inv_shift_left(x: int, bit: int, mask: int = 0xffffffff) -> int:
    tmp = x
    for _ in range(32 // bit):
        tmp = x ^ tmp << bit & mask
    return tmp


def rev_extract(y: int) -> int:
    y = inv_shift_right(y, 18)
    y = inv_shift_left(y, 15, 4022730752)
    y = inv_shift_left(y, 7, 2636928640)
    y = inv_shift_right(y, 11)
    return y


def exp_mt19937(output: list) -> int:
    assert len(output) == 624
    cur_stat = [rev_extract(i) for i in output]
    r = Random()
    r.setstate((3, tuple([int(i) for i in cur_stat] + [624]), None))
    return r.getrandbits(32)


io = remote('39.106.16.204', 24259)
io.recvuntil(b':')
aes_cipher = bytes.fromhex(io.recvline().strip().decode())
io.sendlineafter(b':', b'')
msg = []
for _ in range(30000):
    io.recvuntil(b'[+]')
    msg.append(int(io.recvline().strip().decode()))

io.close()
msg = [msg[i:i + 2500] for i in range(0, 30000, 2500)]

d1 = []
for dx in range(12):
    cp = msg[dx]

    mt = matrix(ZZ, 21, 21)
    for i in range(20):
        mt[i, i] = cp[-1]
        mt[-1, i] = cp[i]
    const = 2 ** 30
    mt[-1, -1] = const
    mt = mt.LLL()

    temp = abs(mt[0, -1])
    assert temp % const == 0

    q0 = temp / const
    e0 = ZZ(cp[-1] % q0)
    p = ZZ((cp[-1] - e0) / q0)

    d1.append(list(map(lambda x: x % p % 256, cp)))

d2 = b''

for dx in range(12):
    ran_output = [bytes_to_long(bytes(d1[dx][i:i + 4])) for i in range(0, 2496, 4)]
    invmul_key = [pow(i, -1, 0x101) for i in long_to_bytes(exp_mt19937(ran_output[::-1]))]

    res = []
    for i in range(4):
        res.append(invmul_key[i] * d1[dx][-4 + i] % 0x101)

    assert all(0 <= i < 4 for i in res)
    res.reverse()
    d2 += bytes([reduce(lambda x, y: 4 * x + y, res)])

print(unpad(AES.new(md5(d2).digest(), AES.MODE_ECB).decrypt(aes_cipher), 16).decode())

Arcahv

Delightful.

from Crypto.Util.number import *
from os import urandom,getenv
from functools import reduce
from Crypto.Cipher import AES

class LCG:
    def __init__(self,seed:int) -> None:
        self.p = getPrime(1024)
        self.a = getPrime(1023)
        self.b = getPrime(1023)
        self.status = seed

    def next(self) -> int:
        ret = self.status
        self.status = (self.status * self.a + self.b) % self.p
        return ret
    
def crystal_trick(m:bytes) -> bytes:
    m = bytearray(m)
    for i in range(len(m)):
        m[i] = reduce(lambda x,y: x^y^urandom(1)[0],m[:i],m[i])
    return m

class RSA:
    def __init__(self):
        p = getStrongPrime(1024)
        q = getStrongPrime(1024)
        self.p = p
        self.N = p * q
        self.e = 65537
        self.d = pow(self.e, -1, (p-1)*(q-1))

    def encrypt(self,m:int) -> int:
        return pow(m,self.e,self.N)
    
    def decrypt(self,c:int) -> int:
        return pow(c,self.d,self.N) 

class MyRSA1(RSA):
    def encrypt(self,m:bytes) -> bytes:
        return super().encrypt(int.from_bytes(m)).to_bytes(256)
    
    def decrypt(self,c:bytes) -> bytes:
        return super().decrypt(int.from_bytes(c)).to_bytes(256)

class MyRSA2(RSA):
    def encrypt(self,m:bytes) -> bytes:
        return pow(int.from_bytes(m),self.e,self.N).to_bytes(256,'little')
    
    def decrypt(self,c:bytes) -> bytes:
        m = pow(int.from_bytes(c),self.d,self.N).to_bytes(256,'little')
        print('Hibiscus is here to trick your decryption result!!')
        return crystal_trick(m)

menu = '''
Welcome to NCTF 2025 arcahv challenge!

--- Menu ---
[1] View encrypted flag and hint
[2] Play with the decryption orcale
[3] Get some random numbers for fun
[4] Exit

Your Option > '''


if __name__=='__main__':
    print('Loading, please wait...')
    
    # flag = open('flag.txt').read().strip().encode()
    flag = getenv('FLAG').encode()
    attempts = 75
    r1 = MyRSA1()
    r2 = MyRSA2()
    hint1 = r2.encrypt(r1.p.to_bytes(128))

    key = urandom(16)
    hint2 = AES.new(key,AES.MODE_ECB).encrypt(r1.N.to_bytes(256))

    def flag_and_hint():
        print(f'Encrypted flag: {r1.encrypt(flag).hex()}')
        print(f'Hint1: {hint1.hex()}')
        print(f'Hint2: {hint2.hex()}')

    def rsachal(): 
        global attempts

        print("Since you didn't v Hibiscus 50 on crazy thursday, Hibiscus decided to do some trick on your decryption result!")
        print(f'Your pubkey:({hex(r2.N)[2:]},{hex(r2.e)[2:]})')

        while attempts > 0:
            if input('Do you still want to try decryption(y/[n])?') != 'y':
                break

            c = bytes.fromhex(input(f'You have {attempts} remaining access to decryption orcale!\nYour ciphertext(in hex):'))
            print(f'Result: {r2.decrypt(c).hex()}')
            attempts -= 1
        
        if attempts == 0:
            print('Unfortunately, you are out of decryption attempts! Come back again on nctf2026 ~')

    
    def lcgchal():
        lcg = LCG(int.from_bytes(key))

        print('Tempering with LCG generator, please wait...')
        while urandom(1)[0] & 0xff:
            lcg.next()
        
        hexnums = ''.join(hex(lcg.next())[2:] for _ in range(5))
        if len(hexnums) % 16:
            hexnums = hexnums.zfill((len(hexnums) // 16 + 1) * 16)
        
        idx = 0
        while input('Do you want another unsigned long long number(y/[n])?') == 'y':
            print(int(''.join(hexnums[idx:idx+16]),16))
            idx = (idx + 16) % len(hexnums)

    def bye():
        print('Hope you have fun during the challenge XD:)')
        exit(0)

    fundc = {1:flag_and_hint,2:rsachal,3:lcgchal,4:bye}

    while True:
        opt = input(menu)
        if len(opt) == 0 or opt not in '1234':
            opt = '4'
        fundc[int(opt)]()

很麻烦，感觉很麻烦。感觉可以分成两道题了。
wp里也说了这是大杂烩，你能看到RSA LSB Orcale,LCG,Coppersmith。
这题比赛时也是只有大致的思路，具体攻击不会。
题目大致可以分成2部分，第一部分的RSA，通过RSA LSB Orcale来获得r1.p。
第二部分就是LCG，LCG生成的数的16进制的长度基本可以认为长度是256，有可能会出现255长度的情况，但只要多试一下就可以了。得到数后就是套公式了。
最后解个RSA就可以得到flag了
那么这题主要就是第一部分的RSA LSB Orcale了。
这个我复现的时候也是想了很久，有些地方wp里没有指出来。先把wp放出来。

一点点来看吧。
首先介绍一下乘法同态，说白了就是你将2个密文相乘，再解密，明文也会是2个明文相乘。类似的还有加法同态，只是把乘法换成了加法，你将2个密文相加，再解密，明文也会是2个明文相加。同时具有加法同态和乘法同态的，我们称之为全同态，也就是上面的FHE。
很明显，RSA具有乘法同态，这个稍微推一下就能出来。
那么我们就可以通过改变密文来使解出来的明文乘以一个确定的数。
如果我们将密文乘C*e，那么解出来的明文将会是原来的C倍。
因为这题我们可以得到明文mod 256的结果(256位以上的都被crystal_trick改变了，没办法得到)，所以我们取C为256。
因为m是小于n的，所以我们可以得到256m%256=0，这个在C较小的时候是恒成立的。但当C较大时，也就是说存在一个数a，C=256**a，使得m*C>n，那么这时候就存在等式m'=C*m-k*n(m’是更改密文后解出来的明文的值)，其中k是正数。我们只能得到模256下的值，所以我们对两边模256，得到m'=-k*n (mod 256)，易得k=-m'*n**(-1) (mod 256)
同时我们要明确一点，这里C=256**a的a是使得C*m>n的最小的a，也就是说k不会很大，我们可以认为k<256，也就是说我们可以认为在模256下求出来的k就是k。
所以，我们可以回到最开始的等式C*m=m'+k*n，m'<n，那么C*m就在k*n和(k+1)*n之间。即k*n/256**a<m<(k+1)*n/256**a，我们就得到了m的一个范围。
我们令a=a+1，即密文再乘一个256**e，即在m'=C*m-k*n两边再乘以一个256，我们可以得到256*m'=256*C*m-256*k*n，其中256*m'是有可能大于n的，而解密出来m''是小于n的，有等式m''=256*m'-k2*n，m''+k2*n=256*m'，代回去得到m''+k2*n=256*C*m-256*k1*n，m''=256**(a+1)*m-256*k1*n-k2*n，m''=256**(a+1)*m-(256*k1+k2)*n，重复上述步骤后能得到256*k1+k2 mod 256的值，即k2，k1前面已经得到，所以我们可以再次缩小m的范围，(256*k1+k2)*n/256**a<m<((256*k1+k2)+1)*n/256**a。这样每次都能把m的范围缩小1/256，最后我们可以得到一个足够小的范围，其中左边界和右边界的高600位是相同的，也就是说我们获得了r1.p的高600位信息，在后面LCG里得到了n后用coppersmith可以很容易求出r1.p。
下面我重新整理一下推理的过程

取一个a，C=256**a，使得C*m>n
m'是解密后的明文
m'=C*m-k*n=256**a*m-k*n
m'=-k*n (mod n)
k=-m'*n**(-1) (mod 256)
k=-(m' mod 256)*n**(-1) (mod 256)
再看等式256**a*m=m'+k*n
=>k*n/256**a<m<(k+1)*n/256**a

256*m'=256*C*m-256*k*n
其中:256*m'=m"+k2*n
m"+k2*n=256*C*m-256*k1*n
m"=256*C*m-256*k1*n-k2*n
m"=256*C*m-(256*k1+k2)*n
m"=-(256*k1+k2)*n (mod 256)
256*k1+k2=-m"*n**(-1) (mod 256)
k2=-(m" mod 256)*n**(-1) (mod 256)
再看等式256**(a+1)*m=m"+(256*k1+k2)*n
=>(256*k1+k2)*n/256**(a+1)<m<((256*k1+k2)+1)*n/256**(a+1)

这里给出我复现的脚本:

from Crypto.Util.number import *
from functools import reduce
from os import urandom,getenv

def crystal_trick(m:bytes) -> bytes:
    m = bytearray(m)
    for i in range(len(m)):
        m[i] = reduce(lambda x,y: x^y^urandom(1)[0],m[:i],m[i])
    return m

class RSA:
    def __init__(self):
        p = getStrongPrime(1024)
        q = getStrongPrime(1024)
        self.p = p
        self.N = p * q
        self.e = 65537
        self.d = pow(self.e, -1, (p-1)*(q-1))

    def encrypt(self,m:int) -> int:
        return pow(m,self.e,self.N)
    
    def decrypt(self,c:int) -> int:
        return pow(c,self.d,self.N) 

class MyRSA1(RSA):
    def encrypt(self,m:bytes) -> bytes:
        return super().encrypt(int.from_bytes(m)).to_bytes(256)
    
    def decrypt(self,c:bytes) -> bytes:
        return super().decrypt(int.from_bytes(c)).to_bytes(256)

class MyRSA2(RSA):
    def encrypt(self,m:bytes) -> bytes:
        return pow(int.from_bytes(m),self.e,self.N).to_bytes(256,'little')
    
    def decrypt(self,c:bytes) -> bytes:
        m = pow(int.from_bytes(c),self.d,self.N).to_bytes(256,'little')
        print('Hibiscus is here to trick your decryption result!!')
        return crystal_trick(m)


attempts = 75
r1 = MyRSA1()
r2 = MyRSA2()

hint1 = r2.encrypt(r1.p.to_bytes(128))

e=r2.e
n=r2.N

c=bytes_to_long(hint1[::-1])
c=c*pow(pow(256,e,n),127,n)%n
k=0
for i in range(attempts):
    c=c*pow(256,e,n)
    p=bytes_to_long(r2.decrypt(long_to_bytes(c))[::-1])
    k=k*256+(-inverse(n,256)*p%256)
    
print(k*n<=r1.p*256**202<=(k+1)*n)
#True

left=k*n//256**202
print(left)
#130885664743289933041962413621767865441591321317558885014199074466855996631539798687727640403945760110268413946434133511019400476370469967300594876528558048910115238902971140792455911038756167472065922832612114808088205280482352816705878339397975785484133224023653016197364452594597283624017262470813673995009

right=(k+1)*n//256**202
left=bin(left)[2:]
right=bin(right)[2:]
for i in range(len(left)):
    if left[i]!=right[i]:
        print(i+1)
        break
print(1024-i-1)
#433

p=130885664743289933041962413621767865441591321317558885014199074466855996631539798687727640403945760110268413946434133511019400476370469967300594876528558048910115238902971140792455911038756167472065922832612114808088205280482352816705878339397975785484133224023653016197364452594597283624017262470813673995009
n=22404304571663619533801749171851644355131031548896050596784492860131952108418133799362203562452927755672086256671456886275374200290455900981573098592802256957759447612198108603737786271333540992054310231142238002312019309261407284535898443221193784771270772676264595891893528938890406282960473610037440992613094585895090383508341010089438083413545705058441072109863024324482039164643863226495180994062873842889196325037541415051411994025140102929000241053770118516405280808187203883977272655025293179259881406034169473289536962089680084335406639749490203495720187657339642405381585747883680749867717205896873223051129

bit=433
R.<x>=PolynomialRing(Zmod(n))
f=p+x
f=f.monic()
roots=f.small_roots(X=2^bit,beta=0.4)
print(roots)

[6941661959252282301910494977227763113291421486720572265514320326916996337372195724367188176400540935900844813645952855916156047100]

上面我只是假设已经得到n了。
所以接下来我们来逆向LCG来得到n
自己稍微改改源码把LCG的5个数的hex给print出来，你会发现在大部分情况下的长度都是256，只有少数情况下会遇到长度是255的，遇到这种情况直接重新获取一下就好了。之后就是套公式恢复参数了。
这里直接贴wp了

得到了n后就可以用上面的coppersmith解出p，然后解RSA1就可以了。
官方wp:

#sage
__import__('os').environ['TERM'] = 'xterm'

from sage.all import *
from pwn import *
from Crypto.Util.number import *
from Crypto.Cipher import AES


def hexify_send(num: int) -> bytes:
    return long_to_bytes(num).hex().encode()

io = remote('39.106.16.204', 28575)
# io = process(['python3', 'arcahv.py'])

io.sendlineafter(b'>', b'1')

io.recvuntil(b':')
enc_flag = int(io.recvline().strip().decode(), 16)
io.recvuntil(b':')
enc_hint = int.from_bytes(bytes.fromhex(io.recvline().strip().decode()), 'little')
io.recvuntil(b':')
enc_hint2 = bytes.fromhex(io.recvline().strip().decode())

# RSA LSB Orcale

m = enc_hint
omit_count = 127
io.sendlineafter(b'>', b'2')
io.recvuntil(b'(')
rn = int(io.recvuntil(b',', drop=True).strip().decode(), 16)
re = int(io.recvuntil(b')', drop=True).strip().decode(), 16)

upper_bound = reduce(lambda x, y: floor(x / 256), range(omit_count), rn)

lower_bound = 0
single_mul = pow(256, re, rn)
inv = pow(rn, -1, 256)

m = m * pow(single_mul, omit_count, rn) % rn

for i in range(75):
    m = int(m * single_mul % rn)
    io.sendlineafter(b'?', b'y')
    io.sendlineafter(b':', hexify_send(m))
    io.recvuntil(b':')
    this = int(io.recvline().strip().decode()[:2], 16)
    k = int(-this * inv % 256)
    ttl = (upper_bound - lower_bound) / 256
    lower_bound += ceil(k * ttl)
    upper_bound = lower_bound + floor(ttl)

res_pp = lower_bound

# LCG

io.sendlineafter(b'>', b'3')
ls = []
for _ in range(80):
    io.sendlineafter(b'?', b'y')
    ls.append(int(io.recvline().strip().decode()))


hexstr = ''.join(hex(i)[2:].zfill(16) for i in ls)
lcgnums = [int(hexstr[i:i + 256], 16) for i in range(0, len(hexstr), 256)]


A = [lcgnums[i + 1] - lcgnums[i] for i in range(4)]
p = gcd(A[1] ** 2 - A[2] * A[0], A[2] ** 2 - A[3] * A[1])

if not isPrime(p):
    p = factor(p)[-1][0]
assert isPrime(p)

a = int(A[1] * int(pow(A[0], -1, p)) % p)
b = int((lcgnums[1] - a * lcgnums[0]) % p)

cur = Zmod(p)(lcgnums[0])
count = 0
while int(cur).bit_length() > 128:
    cur = (cur - b) * pow(a, -1, p)
    count += 1

key = int(cur).to_bytes(16, 'big')
res_n = int.from_bytes(AES.new(key, AES.MODE_ECB).decrypt(enc_hint2), 'big')

# Coppersmith
P.<x> = Zmod(res_n)[]
rt = (res_pp + x).small_roots(X=2 ** 453, beta=0.4)[0]

p0 = int(res_pp + rt)

assert res_n % p0 == 0
q0 = res_n // p0
d0 = int(pow(65537, -1, (p0 - 1) * (q0 - 1)))
print(long_to_bytes(int(pow(enc_flag, d0, res_n))))

至此，三到题已经全部复现。剩下还有三题应该不会去复现了，我也没有去做过。
总得来说这次的NCTF的强度还是有点高的，内容也是非常的多。
那么就这样吧。